箱梁模板的設計中的優化約束方法
2013-06-20 by:廣州有限元分析、培訓中心-1CAE.COM 來源:仿真在線
一.引言
機械優化設計是以最低的成本獲得最好的效益.是設計工作者一直追求的目標,從數學的觀點看。工程中的優化問題,就是求解極大值或極小值問題,亦即極值問題。優化設計是以建立數學模型進行設計的。優化設計引用了一些新的概念和術語,如前所述的設計變量、目標函數、約束條件等。機械優化設計將機械設計的具體要求構造成數學模型,將機械設計問題轉化為數學問題。構成一個完整的數學規劃命題。逐步求解這個規劃命題,使其最佳地滿足設計要求,從而獲得可行方案中的最優設計方案。
機構運動參數的優化設計是機械優化設計中發展較早的領域,不僅研究了連桿機構、凸輪機構等再現函數和軌跡的優化設計問題。而且還提出一些標準化程序。機械零、部件的優化設計最近十幾年也有很大發展。主要是研究各種減速器的優化設計、液壓軸承和滾動軸承的優化設計以及軸、彈簧、制動器等的結構參數優化。除此之外,在機床、鍛壓設備、壓延設備、起重運輸設備、汽車等的基本參數、基本工作機構和主體結構方面也進行了優化設計工作。 近年來發展起來的計算機輔助設計(CAD)引入優化設計方法后。把優化設計方法與計算機輔助設計結合起來,使設計過程完全自動化,已成為設計方法的一個熏要發展趨勢。機械優化設計研究的發展情況表明,機械優化設計已陸續用到建筑結構、化工、冶金、鐵路、航天航空、造船、機床、汽車、自動控制系統、電力系統以及電機、電器等工程設計領域。并取得了顯著效果。
多維有約束優化是在優化問題中最普遍的問題,它的基本形式是,有一個目標函數F(x),數個約束條件。用公式描述如下:
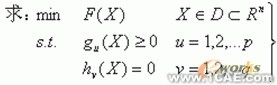
在式中,X為N維向量,表示所需求得的未知量。G(x)與H(x)為兩種不同形式的約束條件。通過對未知向量X的求解,可得到問題的最優解以實現獲得最低成本的最優收益。
本文的問題是某工廠箱梁模版的優化設計,大型的箱梁預制要求機械化程度高,操作方便,其中箱梁內模設計是關鍵。本問題是對24m單線箱梁內模板的設計加工。通過對彎曲位置X,Y和彎曲角度的約束優化,求得內模可下降的最大距離H。通過使用了坐標輪換法和罰函數兩種方法實現了優化的運算。在實際問題中,不僅需要考慮可下降的距離H,還需考慮強度的校合等問題,但由于篇幅有限,得到數據不全,僅以最大距離H來作為最優函數進行求解。
二.問題的描述
箱梁內模的結構為無底式,其具體形狀見圖1,其中,未知量為X,Y, 以知量為:a,b,c,d,e,f,g,h,m。X為第一次動作中模版轉動的位置,
為轉動角度,Y為第二次動作中模版轉動的位置,
為轉動角度。
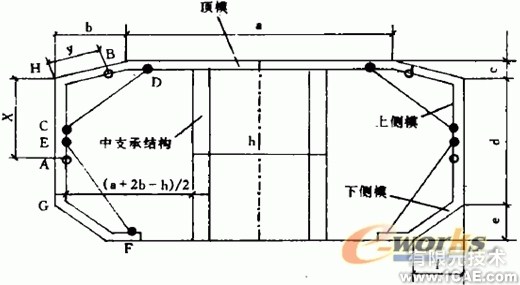
圖1:內模斷面結構圖
箱體梁模的四個動作步驟:
① 收下側模;
② 收上側模;
③ 收頂部油缸,內模整體下降;
④ 通過外設卷揚機將內模拉出預制梁箱體。
通過這4步驟中的前3步建立約束條件。
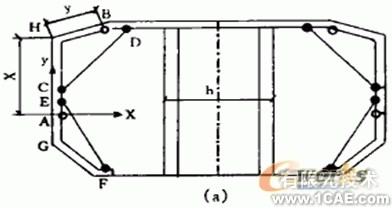
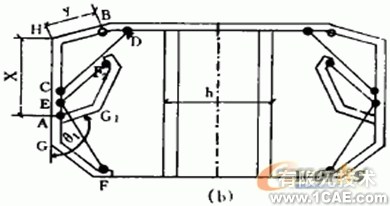
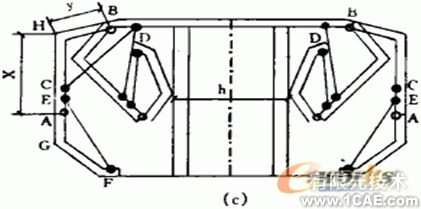
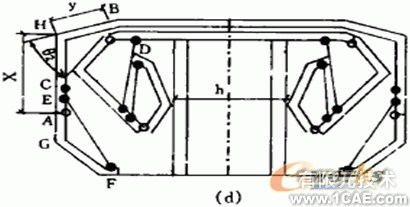
圖2:箱體的三個運動過程
首先,在靜止條件時可得到X,Y的約束條件:
說動作一:收下側模,以A點為中心,將下模旋轉角度,在旋轉過程中,為了避免碰撞
。其中
。
這時F1點坐標
Gl點坐標
其中:AG=(d—x)
動作二:收上側模,以B點為中心,將上側模(此時下側模與上側模連為一體,為剛性體。)旋轉角度,在旋轉過程中,要求G點的橫坐標Xg2<(a+2b-h)/2,同時H點橫坐標XH>g。
動作三:內模整體下降,在此過程中,G1點的Y軸位置應該更大。即:XYcosarctg( /
)值最大。這樣可以得到所有的約束條件和所需函數:

三.多維約束優化
1.方法的描述
多維優化分為直接和間接法兩種。
在直接法中,每一步的迭代解都要服從兩個條件——可行性和使用性。
解的可行性是指每一步的迭代解都應當在可行域的范圍之類。
解的使用性是指每一步的迭代解都應當是較上一值更優的。(在某些方法中,會以一定概率接受次解以增加解的可能性)
本文使用的輪換法就是一種典型的直接優化方法。
間接法是指通過一定的方法將優化問題轉換,使期去除約束,成為無約束優化問題,從而使用無約束優化的方法來解決。其中,懲罰函數法為較為常用的間接法。
2.輪換法的敘述
一般問題的可行域為:
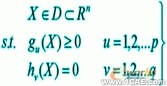
在約束范圍中當存在某個點X*,使其周圍每個點當距離小于某e>0時,f(x)<f(X*)。則我們稱:X為一個局部最優解。在一個問題中,可能存在數個局部最優解。
全局最優解為所求問題中整體的最小值,即我們所欲求得的值,全局最優解一定在局部最優解中,故,只需在局部最優解中尋找最小值即可。
輪換法為一種直接求解的有約束優化方法,其建立在多維無約束優化方法的基礎上。基本思想為:尋找某維上的最小值直至找到或超出范圍,換維繼續尋找,直至到達終止條件。步驟可以簡單描述:
1.選取一個步長a,初始值x(0)和終止條件e
2.沿x(0)中的第一維方向進行搜索,其初始步長為a,
3.當x(0)的第一維方向以a=2a的速度進行搜索,直至f(x)開始增大(既找到局部最優解)或x超出約束條件
4.退回當前步長a,將此x(0)的第一維方向記做x(1)的第一維方向,增加一維從新進行2-4步過程。
5.當x(0)達到其最大維數,使用所記錄的x(1)進行新的搜索,此時,a=a/2
6.如此循環直至達到終止條件
其流程圖基本如下:
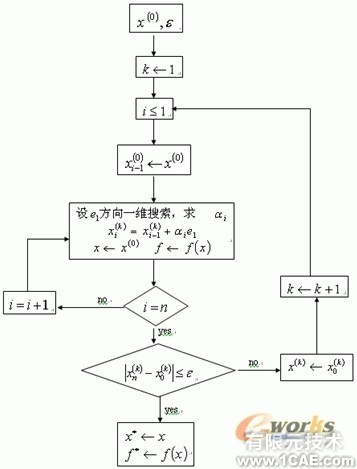
圖3:輪換坐標法的流程圖
3.懲罰函數法
懲罰函數法是一種間接求解的多維有約束優化算法,它的數學模型與輪換法類似,不過,引入了一個新的條件,罰函數:
此罰函數須滿足兩個條件:
1.不破壞原函數的約束條件
2.取最小值時的x因為f(x)取最小值時的x
通過引入罰函數,原問題變成了高維的無約束優化問題,可以使用無約束優化方法進行求解。
具體步驟如下:
1.在可行域內選擇初始點x0, x0的選擇可根據經驗選擇
2.確定初始罰因子r0和C,并確定K值為0。
3.求罰函數的最小值,解出最優點Xk
4.當K=0時,跳至步驟5,否則至6
5.xk+1=xk,轉至步驟3
6.判斷終止條件,滿足則繼續到7,否則至步驟5
7.輸出f(x)與x
其路程圖大致如下:
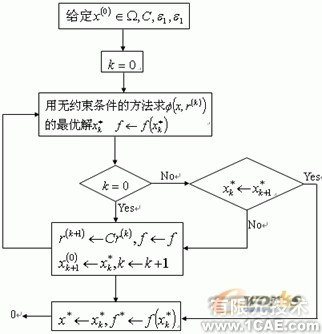
圖4:罰函數法的流程圖
結束條件通常有兩個,一為兩次的X值的變化較小,即,二為兩次的F(x)值變化較小,即
四.問題的實際應用
在實際問題中,應當先建立正確的模型以進行進一步的分析。
在第二節中,對問題的分析后給出的數學模型建立如下:

其中,X,Y, ,
作為未知量進行輪換,而下面四個為約束條件,函數F(x)是個求最大值的函數,故可將F(x)=-F(x)。
使用輪換坐標法對其進行優化,將X(X,Y, ,
)作為坐標四維向量進行輪換運算。當達到結束條件時,可終止運算。
對模型的建立,罰函數法與坐標輪換法基本一致,均使用在第二節中分析出的目標函數和約束條件,在運算時,需使罰函數用(x)的形式表示。即
(因為約束條件為4個,且只存在
的形式。使用此罰函數進行多維無約束優化運算,達到終止條件時對其終止,可得到優化結果。
五.結論
通過使用坐標輪換法對箱體的壓模進行設計后,得到了較好的結果,雖然同實際的結果存在著一定的差異,因為在實際工作中,需考慮到物體的強度等更多的因素,需增加更多的約束條件。
從整體看來,機械優化是一種先進有效的優化方法,它有效的運算了在多維有約束的條件下,機械設計的最優解的求得。在各個領域里均得到了廣泛的運用,有效的提高了產品的質量與設計。
并且,隨著對運算要求的不斷提高,更多的優化方法也被提出,如,遺傳算法,模擬退火算法,神經網絡算法,蟻群算法。這些方法更能快速有效的提高了優化的運算,為機械的設計提供了更好的工具。
相關標簽搜索:箱梁模板的設計中的優化約束方法 Fluent、CFX流體分析 HFSS電磁分析 Ansys培訓 Abaqus培訓 Autoform培訓 有限元培訓 Solidworks培訓 UG模具培訓 PROE培訓 運動仿真






