CFD逆天黑科技:“多重網格法”
2017-02-24 by:CAE仿真在線 來源:互聯網
CFD的偏微分方程組離散后需要使用迭代解法來求解,比較常用的求解方法有高斯賽德爾點迭代法、雅克比點迭代法等(參考:可否認真的考慮過什么是CFD中的殘差?為什么殘差都是小數?)。隨后,不同的Krylov子空間方法成功逆襲被應用到CFD中。
但是,Krylov子空間方法的一個致命問題即為當稀疏線性系統變得非常大的時候,收斂速度會變慢。這種迭代速率的變慢,每一步操作數的增加造成了嚴重的效率損失。
下圖是采用普通的迭代算法求解10*10矩陣,20*20矩陣,40*40矩陣的收斂速度對比(CFD界:H.K. Versteeg在原著中并沒有表示是采用了什么迭代算法...)。很明顯的,40*40矩陣的收斂速度在大約100次迭代后嚴重放緩。
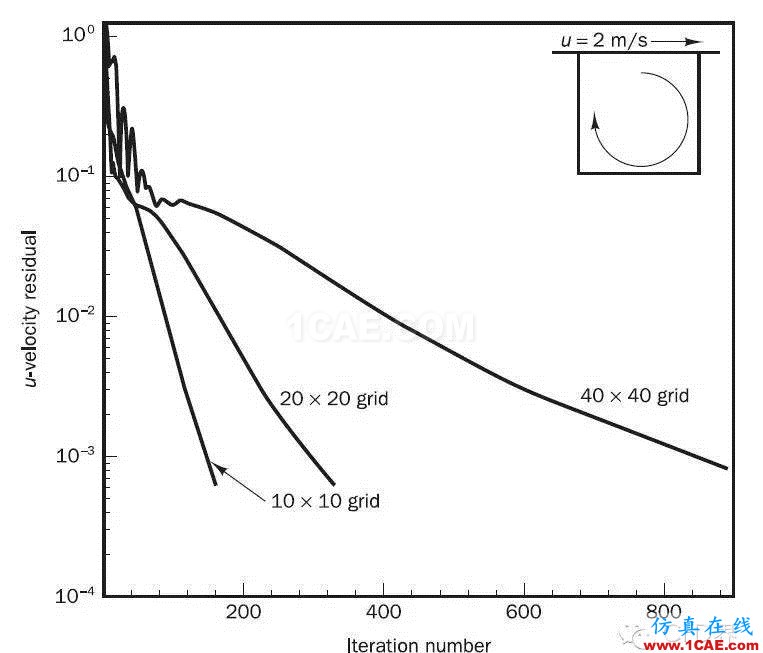
多重網格針對這種求解系統越大,收斂越慢的問題而生!
早期的多重網格方法可以追溯到60年代。然而,在70年代末和80年代初期多重網格法才出現各種變種。Brandt是多重網格的先驅者。他在多重網格中引入了各種關鍵技術(至今仍然廣泛采用),并且和當時現存的求解方法相對比,充分的展示了多重網格法的優越性。隨后,代數多重網格法被提出。
時至今日,多重網格法依然是求解橢圓PDE最有效的方法。然而,多重網格法依然存在一些缺陷,因此對多重網格法的研究從未停止。因為計算機能力越來越強,這種收斂速度和網格大小無關的算法越來越重要。
多重網格求解技術需要在不同的粗細量級的網格上對同一個原始的PDE方程進行求解。舉個栗子:
-
我們首先在40*40網格上對PDE方程進行離散,然后在這個10*10網格上求解n1次
-
將PDE方程離散到20*20的網格上,進行n2次迭代
-
將PDE方程離散到10*10的網格上,進行n3次迭代
-
將10*10的網格上求得的解,重組到20*20網格,進行n4次光順
-
將20*20的網格上求得的解,重組到40*40網格,進行n5次光順
上述過程就完成了多重網格求解的一次循環。由于多重網格法是極為、非常、相當復雜的。關于如何正確地對方程進行操作和計算,CFD界在這里就不介紹了。
CFD大牛?一測便知
Q4:
理論上,如果計算網格無限大,不管使用什么格式,對傳輸方程離散后的數值解會和精確解完全一樣。然而,在CFD計算中我們僅僅使用有限的、非常少的網格來計算。在這種情況下,要保持解的正確。格式需要具有以下特點:守恒性、_____、傳輸特性。
回復q4至CFD界獲取答案
原版內容取自,額,各大CFD教材,并由CFD界整理
相關標簽搜索:CFD逆天黑科技:“多重網格法” Fluent培訓 Fluent流體培訓 Fluent軟件培訓 fluent技術教程 fluent在線視頻教程 fluent資料下載 fluent分析理論 fluent化學反應 fluent軟件下載 UDF編程代做 Fluent、CFX流體分析 HFSS電磁分析






